Prim algoritmusa

Ebben az oktatóanyagban megtudhatja, hogyan működik a Prim algoritmusa. Ezenkívül találni működő példákat a Prim algoritmusára C, C ++, Java és Python nyelven.

A Prim algoritmusa egy minimális átívelő fa algoritmus, amely egy gráfot vesz be bemenetként, és megtalálja a gráf széleinek azon részhalmazát, amely

alkot egy fát, amely minden csúcsot tartalmaz
megadja a minimális súlyösszeget az összes fa között, amely a grafikon alapján kialakítható

Hogyan működik Prim algoritmusa

A kapzsi algoritmusoknak nevezett algoritmusok osztályába tartozik, amelyek megtalálják a lokális optimumot abban a reményben, hogy globális optimumot találnak.

Egy csúcsból indulunk, és folyamatosan adjuk hozzá a legkisebb súlyú éleket, amíg el nem érjük célunkat.

A Prim algoritmusának megvalósításának lépései a következők:

A véletlenszerűen kiválasztott csúccsal inicializálja a minimális fát.
Keresse meg az összes élt, amely összeköti a fát új csúcsokkal, keresse meg a minimumot, és adja hozzá a fához
Addig ismételje a 2. lépést, amíg meg nem kap egy minimális átfogó fát

Példa Prim algoritmusára

Kezdjük egy súlyozott gráf

Válasszon egy vertex

Válassza a legrövidebb él ebből vertex és add meg

kiválasztani a legközelebbi csúcs még nincs megoldás

Válassza ki a legközelebbi széle még nem a megoldás, ha több választási válasszon egyet véletlenszerűen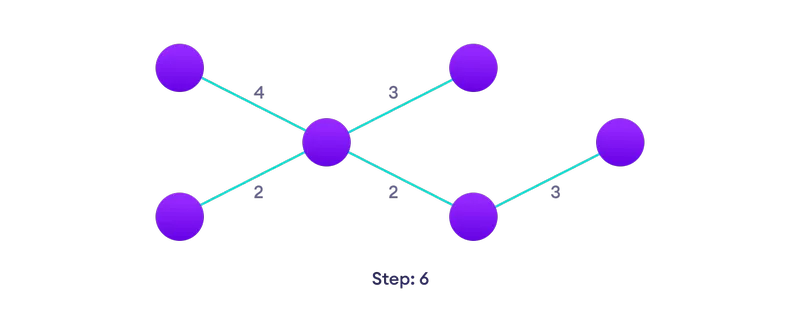

ismételje, amíg meg nem legyen egy átfogó fája

Prim algoritmus álkódja

A prim algoritmusának álkódja megmutatja, hogyan hozunk létre két U és VU csúcs halmazt. Az U tartalmazza a meglátogatott csúcsok listáját, a VU pedig a még nem vett csúcsok listáját. A legkisebb súlyú él összekötésével egyesével mozgatjuk a csúcsokat a JE és U között.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Példák Python, Java és C / C ++

Noha a grafikonok szomszédsági mátrix ábrázolását használják, ez az algoritmus az Adjacency List használatával is megvalósítható annak hatékonyságának javítása érdekében.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Prim vs Kruskal algoritmusa

Kruskal algoritmusa egy másik népszerű minimális átívelő fa algoritmus, amely más logikát használ a gráf MST megtalálásához. Ahelyett, hogy egy csúcsból indulna ki, Kruskal algoritmusa az összes élt az alacsony súlytól a nagyig rendezi, és folyamatosan a legalacsonyabb éleket adja hozzá, figyelmen kívül hagyva azokat az éleket, amelyek ciklust hoznak létre.